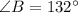Question

Quadrilateral ABCD ​ is inscribed in this circle.

What is the measure of angle B?

Enter your answer in the box.

m∠B=
°

A quadrilateral inscribed in a circle. The vertices of the quadrilateral lie on the edge of the circle and are labeled as A, B, C, D. The interior angle B is labeled as left parenthesis 3 x minus 12 right parenthesis degrees. The angle D is labeled as x degrees.

Answer 1

The measure of angle B is 132°

Step-by-step explanation:

Given that the quadrilateral is inscribed in a circle.

The vertices A, B, C, D of a quadrilateral lie on the edge of the circle.

The angle B is given by
`\angle B=(3x-12)^(\circ)`

The angle D is given by
`\angle C=x^(\circ)`

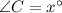
We need to find the measure of angle B.

Since, the angles B and D are opposite angles.

Also, we know that the opposite angles of a quadrilateral are supplementary.

Thus, we have,

`\angle B+\angle D=180^{\circ`

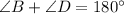
Substituting the values, we get,

`3x-12+x=180`

`4x-12=180`

`4x=192`

`x=48`

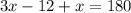
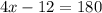
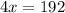
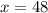
Thus, the value of x is 48

Substituting the value of x in the angle B, we get,

`\angle B=(3(48)-12)^(\circ)`

`\angle B=(144-12)^(\circ)`

`\angle B=132^(\circ)`

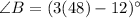
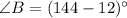
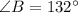
Thus, the measure of angle B is
`\angle B=132^(\circ)`