Question

Quadrilateral ABCD ​ is inscribed in this circle.

What is the measure of angle A?



Enter your answer in the box.


°

A quadrilateral inscribed in a circle. The vertices of the quadrilateral lie on the edge of the circle and are labeled A, B, C, D. The interior angle A is labeled as left parenthesis 2 x plus 1 right parenthesis degrees. The angle B is labeled as 148 degrees. The angle D is labeled as x degrees.

Answer 1

Here are the correct answers, sorry if you had different questions.

Step-by-step explanation:

Answer 2

The measure of angle A is 65°

Step-by-step explanation:

Given that ABCD is a quadrilateral inscribed in a circle.

The measure of angle A is
`\angle A=(2x+1)^(\circ)`

The measure of angle B is
`\angle B=148^(\circ)`

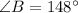
The measure of angle D is
`\angle D=x^(\circ)`

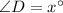
We need to determine the measure of angle A.

Since, we know that the angles B and D are opposite angles and the opposite angles of a quadrilateral add up to 180°

Thus, we have,

`\angle B+\angle D=180^(\circ)`

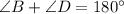
Substituting the values, we have,

`148^(\circ)+x=180^(\circ)`

`x=32^(\circ)`

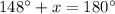
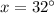
Thus, the value of x is 32°

Substituting the value of x in the measure of angle A, we get,

`\angle A=(2x+1)^(\circ)`

`\angle A=(2(32)+1)^(\circ)`

`\angle A=(64+1)^(\circ)`

`\angle A=65^(\circ)`

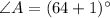
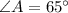
Thus, the measure of angle A is 65°