Question

A piston–cylinder assembly contains air, initially at 2 bar, 300 K, and a volume of 2 m3. The air undergoes a process to a state where the pressure is 1 bar, during which the pressure–volume relationship is pV 5 constant. Assuming ideal gas behavior for the air, determine the mass of the air, in kg, and the work and heat transfer, each in kJ.

Answer 1

Work, W = 277.269kJ

Internal energy, Q = 277.269kJ

Step-by-step explanation:

Given-

Pressure, P1 = 2 bar

Temperature, T1 = 300K

Volume, V1 = 2m³

P2 = 1 bar

PV = constant

Let,

mass in kg be m

Work in kJ be W

Heat transfer in kJ be Q

R' = 8.314 kJ/kmolK

Mass of air, Mair = 28.97 kg/kmol

R = 0.289 kJ/kgK

We know,

PV = mRT

`m = (P_1V_1)/(RT_1)`

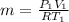
m = 5.65kg

To calculate V₂:

PV = constant = P₁V₁ = P₂V₂

P₁V₁ = P₂V₂

`V_2 = (P_1V_1)/(P_2)`

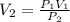
V₂ = 4m³

To calculate the work:

P₁V₁ = C

P₁ = C/ V₁

`W = \int\limits^V_V {pdV} \,`

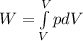
where limit is V₁ to V₂

`W = \int\limits^V_V {(c)/(v) } \, dV \\\\W = C\int\limits^V_V {v^-^1} \, dV\\ \\W = P_1V_1 (ln(V_2)/(V_1) ) \\\\W = (2 bar) (2m^3) (ln(4m^3)/(2m^3)) ((10^5 N/m^2)/(1 bar)) \\\\W = 277.259kJ`

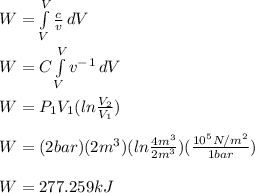
To calculate heat transfer:

Q - W = Δu

Q - W = m (u₂ - u₁)

Q = W + m (u₂ - u₁)

Q = W + m X cv X (T₂ - T₁)

Since, T₁ ≈ T₂

There is no change of internal energy.

W = Q

Q = 277.269kJ