Question

Calculate a 95% confidence interval for the population proportion of people who believe the governor broke campaign financing laws. Does the result of the poll convince you that fewer than 38% of all U.S. citizens favor that viewpoint?

Answer 1

The 95% confidence interval for the population proportion of people who believe the governor broke campaign financing laws is (33%, 39%).

Explanation:

The (1 - α) % confidence interval for population proportion is:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

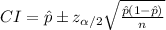
For a 95% confidence interval the critical value of z is:

`z_(\alpha/2)=z_(0.05/2)=z_(0.025)=1.96`

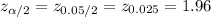
The sample proportion is,
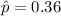`\hat p =0.36` and the sample size is, n = 900.

Compute the 95% confidence interval for the population proportion of people who believe the governor broke campaign financing laws as follows:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}\\=0.36\pm 1.96*\sqrt{(0.36(1-0.36))/(900)}\\=0.36\pm0.03136\\=(0.32864, 0.39136)\\\approx(0.33, 0.39)`

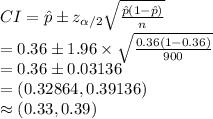
The 95% confidence interval for the population proportion of people who believe the governor broke campaign financing laws is (33%, 39%).

The null hypothesis can be defined as:

H₀: More than 38% of all U.S. citizens favor that viewpoint, i.e. p > 0.38.

As the 95% confidence interval consists of the null value so it can concluded that fewer than 38% of all U.S. citizens favor that viewpoint.