Answer:
98% confidence interval for the mean rate = [4.1437 , 4.4983]
Explanation:
We are given the interest rates (annual percentage rates) for a 30-year fixed rate mortgage from a sample of lenders in Macon, Georgia for one day ;
4.751, 4.373, 4.177, 4.676, 4.425, 4.228, 4.125, 4.251, 3.951, 4.192, 4.291, 4.414
Now, Firstly we will find Mean of above data, Xbar ;
Mean, Xbar =
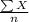 =
=
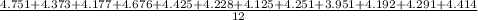 = 4.321
= 4.321
Standard deviation, s =
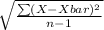 = 0.226
= 0.226
Now, the pivotal quantity for 98% confidence interval for the mean rate is;
P.Q. =
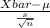 ~
~

where, Xbar = sample mean
s = sample standard deviation
n = sample size = 12
So, 98% confidence interval for the mean rate,
 is ;
is ;
P(-2.718 <
 < 2.718) = 0.98
< 2.718) = 0.98
P(-2.718 <
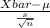 < 2.718) = 0.98
< 2.718) = 0.98
P(Xbar - 2.718 *
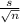 <
<
 < Xbar + 2.718 *
< Xbar + 2.718 *
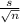 ) = 0.98
) = 0.98
98% confidence interval for
 = [Xbar - 2.718 *
= [Xbar - 2.718 *
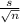 , Xbar + 2.718 *
, Xbar + 2.718 *
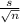 ]
]
= [4.321 - 2.718 *
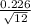 , 4.321 + 2.718 *
, 4.321 + 2.718 *
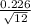 ]
]
= [4.1437 , 4.4983]
Therefore, 98% confidence interval for the mean rate = [4.1437 , 4.4983]