Question

Dodo has twice as many green pencils as red pencils. WHEN DODO LOST 42 green pencils he had half as many greens pencils as red pencils. How many pencils did he have altogether? Please help me this is due tomorrow and I really need it to be done thanks☺️

Answer 1

Dodo initially had 56 green pencils and 28 red pencils.

Explanation:

Step 1:

Assume the number of green pencils is x and the number of red pencils is y. From the question, we have

`x = 2y, x - 2y = 0`, take this as equation 1,

`x-42 = (y)/(2) = 2(x-42) = y, 2x - 84 = y, 2x-y = 84`

`2x-y=84`, take this as equation 2.

Step 2:

If we multiply equation 1 with 2 and subtract it from equation 2, we cancel out the x variable and can solve for the value of y.

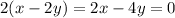`2(x-2y) = 2x - 4y = 0`, take this as equation 3.

By subtracting equation 2 from 3, we get

`-3y = -84, y = (-84)/(-3), y = 28.`

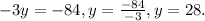
Step 3:

Substituting this value of y in any of the previous equations we will get x's value.

Here this value of y i.e y = 28 is substituted in equation 1.

`x - 2(28) =0, x - 56=0, x = 56.`

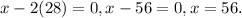
So we have x = 56 and y = 28.