Step-by-step explanation:
Relation between pressure of water and its droplet is as follows.
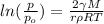
where, p = pressure of droplet
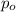 = water pressure in given temperature
= water pressure in given temperature
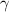 =
=
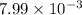
M = Molecular Weight in Kg/Mol (0.018 for water)
r = radius in meters
 = density of water in
= density of water in
 (1000
(1000
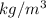 )
)
R = ideal gas constant (8.31)
T = temperature in Kelvin
(a) We will calculate the value of p as follows.
p =

=
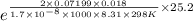
= 26.8 torr
(b) And, vapor pressure of spherical water droplets of radius 2.0
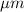 or
or
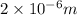
p =

=
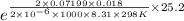
= 25.2 torr