Answer:
a) Z = 426.3 Ω
b) Ф = 35.1°
Step-by-step explanation:
The ac generator has a voltage(Vrms) of 113 V, when connected to a resistor there is a current(Irms) of 0.324 A. The resistance of the resistor(R) is given by:
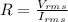
Substituting values:
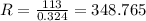
R = 348.765 Ω
When the generator is connector to an inductor the current(Irms) is 0.461 A.
The impedance of the inductor XL is given by:
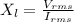
Substituting values:
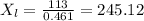
XL = 245.12 Ω
When both the resistor and the inductor are connected in series between the terminals of this generator
(a) the impedance of the series combination
the impedance of the series combination(Z) =
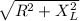
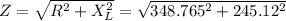 = 426.3 Ω
= 426.3 Ω
Z = 426.3 Ω
(b) the phase angle between the current and the voltage of the generator
the phase angle(Ф) is given by:
tanФ = XL/R
Ф = tan⁻¹(XL/R)
Ф = tan⁻¹(245.12/348.765) = tan⁻¹(0.7028) = 35.1°
Ф = 35.1°