Answer:
Given inequality
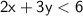
Rearrange to make y the subject
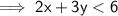
Subtract 2x from both sides:
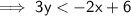
Divide both sides by 3:
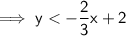
When graphing inequalities
If the inequality sign is < or > then the line of the graph should be dashed.
If the inequality sign is ≤ or ≥ then the line of the graph should be solid.
If y < (less than) then the shading is below the line.
If y > (more than) then the shading is above the line.
Therefore, as the inequality is y < the line should be dashed and the shading should be below the dashed line.
To plot the line, substitute x = 0 and x = 3 into the equation:
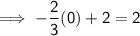
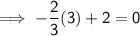
Therefore, plot points (0, 2) and (3, 0). Draw a dashed straight line through the points. Shade below the dashed line.