Question

Suppose that 70% of the orders on a particular website are shipped to the person who is making the order and the remaining 30% are shipped to people other than the person placing the order. Gift wrapping is requested for 60% of the orders being shipped to other people, but for only 10% of orders shipped to the person making the order.

Answer 1

a) P=0.24

b) P=0.31

c) Not independent.

Explanation:

Incomplete question.

a) What is the probability that a randomly selected order will be wrapped and sent to another person?

`P(W\&SOP)=P(SOP)*P(W|SOP)=0.30*0.60=0.24`

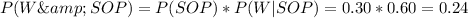
W: wrapped

SOP: sent to other people

b) What is the probability that a randomly selected order will be gift wrapped?

`P(W)=P(SOP)*P(W|SOP)+P(SR)*P(W|SR)\\\\P(W)=0.3*0.6+0.7*0.1=0.24+0.07=0.31`

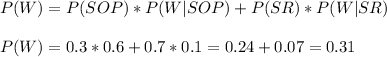
SR: sent to the right person

c) Is gift wrapping independent of the destination of the gift? Justify your response statistically.

To prove that they are independent, both of the following conditions must be met:

• P(x|y) = P(x), for all values of X and Y.

• P(x ∩ y) = P(x) * P(y), for all values of X and Y.

We start for the second condition.

`P(W\cap SR)=0.1\\\\P(W)*P(SR)=0.31*0.7=0.217\\\\\\P(W\cap SR)\\eq P(W)*P(SR)`

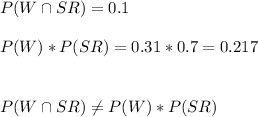
This condition is not met, so the two variables are not independent.