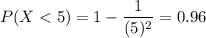Question

Suppose that contamination particle size (in micrometers) canbe modeled as

f(x) = 2x-3 for 1
a) confrm that f(x) is a probability density function.

b) Given the cumulative distribution function.

c) Determine the mean

d) what is the probability that the size of random particle will be less than 5 micrometers?

Answer 1

c) 2

d) 0.96

Explanation:

We are given the following in the question:

`f(x) = 2x^(-3), x > 1\\~~~~~~~= 0, x \leq 1`

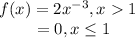
a) probability density function.

`\displaystyle\int^(\infty)_(\infty)f(x) dx = 1\\\\\displaystyle\int^(\infty)_(-\infty)2x^(-3)dx = 1\\\\\displaystyle\int^(\infty)_(1)2x^(-3)dx\\\\\Rightarrow \big[-x^(-2)\big]^(\infty)_1\\\\\Rightarrow -(0-1) = 1`

Thus, it is a probability density function.

b) cumulative distribution function.

`P(X<x) = \displaystyle\int^(x)_(1)2x^(-3)dx\\\\P(X<x)=\big[-(x^(-2))\big]^(x)_(1)\\\\P(X<x)=-\bigg((1)/(x^2)-1\bigg) = 1 - (1)/(x^2)`

c) mean of the distribution

`\mu = \displaystyle\int^(\infty)_(-\infty)xf(x) dx\\\\\mu = \int^(\infty)_12x^(-2)dx\\\\\mu = (-(2)/(x))^(\infty)_(1)\\\\\mu = 2`

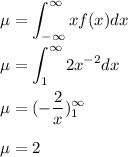
d) probability that the size of random particle will be less than 5 micrometers

`P(X<5)= 1 - (1)/((5)^2) = 0.96`