Question

What does x =
4
9
16

Answer 1

For the given triangle, x = 16 units.

Explanation:

Step 1:

In the given triangle, the angle is 60°. The adjacent side has a length of 8 units while the hypotenuse of the triangle measures x units. To calculate the cos of angle A we divide the length of the adjacent side by the length of the hypotenuse.

cos A
`= (adjacentside)/(hypotenuse).`

Step 2:

The length of the adjacent side = 8 units.

The length of the hypotenuse = x units.

`cos\theta = (adjacentside)/(hypotenuse) , cos 60 = 0.5, cos 60 = (8)/(x) .`

`x = (8)/(cos60) = (8)/(0.5) = 16.`

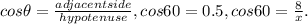
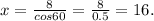
So the hypotenuse of the given triangle measures 16 units. x = 16 units which is the third option.