Question

Can someone please help me thsi the only one i need

Answer 1

a) The explicit formula is
`a_n=7n+5`

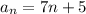
b) The 31st term of the sequence is 222

Explanation:

a) The explicit formula for an arithmetic sequence is:

`a_n=a_1+(n-1)d`

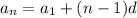
The recursive formula for the sequence is

`a_1=12\\a_n=a_(n-1)+7`

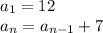
From this formula we can find the common difference by comparing to the general recursive formula:
`\\a_n=a_(n-1)+d`

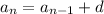
This means the common difference d=7.

We now substitute the first term
`a_1=12` and the common difference
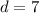`d=7` into the explicit formula:
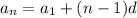`a_n=a_1+(n-1)d` to obtain:

`a_n=12+(n-1)* 7`

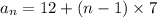
Expand to get:

`a_n=12+7n-7`

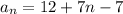
Simplify:

`a_n=7n+5`

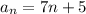
b) To find the 31st term of this sequence, we substitute n=31 in to the the explicit formula,
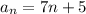`a_n=7n+5` to obtain:

`a_(31)=7*31+5`

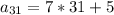
Multiply to get:

`a_(31)=217+5`

Add to get:

`a_(31)=222`

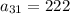
Therefore the 31st term of the sequence is 222