Question

The curves r1(t) = 2t, t2, t3 and r2(t) = sin t, sin 5t, 3t intersect at the origin. Find their angle of intersection, θ, correct to the nearest degree.

Answer 1

The angle between the curves is 80.27°.

Explanation:

Given that

r₁(t) = <2t, t²,t³>

Differentiating with respect to t

r'₁(t) = <2, 2t,3t²>

Since it is intersect at origin.

Then r'₁(0)= <2,0,0> [ putting t=0]

The tangent vector at origin of r₁(t) is

r'₁(0)= <2,0,0>

Again,

r₂(t)= <sin t, sin 5t, 3t>

Differentiating with respect to t

r'₂(t)= <cost, 5 cos 5t, 3>

Since it is intersect at origin.

Then r'₂(0)= <1,5,3> [ putting t=0]

The tangent vector at origin of r₂(t) is

r'₂(0)= <1,5,3>

The angle between the carves is equal to the angle between their tangent.

We know that

`Cos \theta = (r'_1(0).r'_2(0))/(|r'_1(0)||r'_2(0)|)`

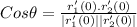
Putting the all values

`Cos \theta = (<2,0,0>.<1,5,3>)/(√(2^2+0^2+0^2)√(1^2+5^2+3^2))`

`\Rightarrow \theta =cos^(-1)((2)/(2√(35)))`

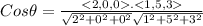
⇒θ= 80.27°

The angle between the curves are 80.27°.