Option D:
Square both sides of the equation is the best way to solve the equation.
Solution:
Given equation:
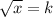
To find which is the best way to solve the equation.
Option A: Multiply both sides of the equation by k.
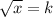
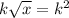
In this method, we are not obtain x value.
It is not true.
Option B: Divide both sides of the equation by k.
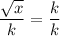
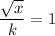
In this method, we are not obtain x value.
It is not true.
Option C: Take the square root of both sides of the equation.
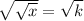
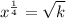
In this method, we are not obtain x value.
It is not true.
Option D: Square both sides of the equation.
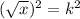
Square and square root get canceled.
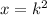
We obtain x value.
It is true.
Therefore square both sides of the equation is the best way to solve the equation.
Option D is the correct answer.