Question

Find the gcf of the following

4x^4y^3 and 24x^3y^2

Answer 1

The greatest common factor (gcf) of
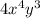`4x^(4)y^(3)` and
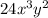`24x^(3)y^(2)` is 4 x³ y²

Explanation:

The greatest common factor of algebraic terms is:

• The greatest common factor of the numbers
• Least exponent of the same variables

Ex: The greatest common factor of 8 x² and 12 x³ is 4 x² because:

The factors of 8 are 1, 2, 4, 8 and the factors of 12 are 1, 2, 3, 4, 6, 12

The common factor of them are 1, 2, 4 and the greatest on is 4

The greatest common factor of x² and x³ is x²

So the gcf of 8 x² and 12 x³ is 4 x²

∵ The terms are
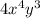`4x^(4)y^(3)` and
`24x^(3)y^(2)`

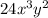
∵ The factors of 4 are 1, 2, 4

∵ The factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24

∴ The common factors of them are 1, 2, 4

∵ The greatest one is 4

∴ The greatest common factor of 4 and 24 is 4

∵ The greatest factor of
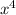`x^(4)` and x³ is x³

∵ The greatest factor of y³ and y² is y²

∴ The greatest common factor of
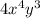`4x^(4)y^(3)` and
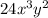`24x^(3)y^(2)` is 4 x³ y²