The time required to lift 1500 tons was estimated.
Step-by-step explanation:
Given data,
Head discharge H = 28-9
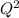
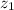 = 2.5 m
= 2.5 m
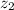 = 7.8 m
= 7.8 m
The suction pipe
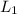 = 16 m
= 16 m
The delivery pipe
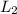 = 764 m
= 764 m
Diameter d = 0.8 m
coefficient of friction f = 0.005
coefficient of friction (km) pump = 1.5
H = 28-9
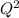
The total head H =
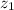 +
+
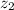 + h
+ h
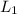 + h
+ h
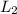
h
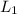 =
=
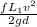
h
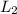 =
=

H =
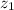 +
+
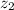 +
+
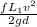 +
+

H = 2.5 + 7.8 +
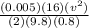 +
+
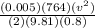
H = 10.3+0.051
 + 2.43
+ 2.43

H = 10.3 + 2.48

28-9
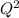 = 10.3 + 2.48
= 10.3 + 2.48

V =
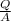 =
=
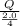 = 2Q
= 2Q