Question

The given line segment has a midpoint at (−1, −2).

On a coordinate plane, a line goes through (negative 5, negative 3), (negative 1, negative 2), and (3, negative 1).

HELP ME PLEASE I DONT KNOW THE ANSWER



What is the equation, in slope-intercept form, of the perpendicular bisector of the given line segment?


y = −4x − 4

y = −4x − 6

y = One-fourthx – 4

y = One-fourthx – 6

Answer 1

y = -4(x) - 6

Explanation:

For anyone looking for a simple answer.

Answer 2

The equation of the perpendicular line is y = −4(x) − 6

Explanation:

Given:

Three coordinates points (in pair).

Lets choose two points,in
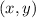`(x,y)` format.

Where

`(x,y)` =
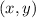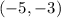`(-5,-3)` and
`(x_1,y_1)` =
`(3,-1)`

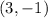
From these points we will find the slope using point-slope formula.

That is :

`(y_1-y)=m(x_1-x)`

`m=((y_1-y))/((x_1-x))`

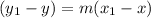
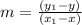
Plugging the values:

`m=(-1+3)/(3+5)=(1)/(4)`

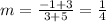
Now we know that product of slope of two perpendicular lines = -1.

So the slope of the line which is perpendicular
`(m_1)` .

`m_1=(-1)/(m)`

`m_1=(-1)/((1)/(4) ) =-1* (4)/(1) =-4`

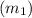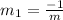
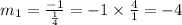
Now using this slope we will plug the midpoint (-1,-2) values in point-slope form and reduced it to slope intercept.

`y-(-2)=-4(x+1)`

`y+2=-4x-4`

`y=-4x-4-2`

`y=-4x-6`

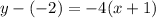
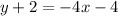
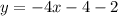
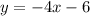
So the equation of the perpendicular bisector is y = -4(x) - 6