Answer:
The voltage in exponential form would be
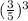 .
.
The original voltage in the circuit is
 of a volt.
of a volt.
Explanation:
Let x represent the original voltage.
We have been given that the voltage in an electrical circuit is multiplied by itself each time it is reduced. The voltage is 27/125 of a volt and it has been reduced 3 times.
The original voltage multiplied by itself for 3 times would be
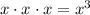 .
.
Now, we will equate
 with 27/125 as:
with 27/125 as:
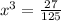
We know that 27 is cube of 3 and 125 is cube of 5, so we can represent our equation as:
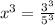
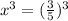
Therefore, the voltage in exponential form would be
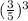
Now, we will take cube root of both sides to find original voltage in the circuit as:
![\sqrt[3]{x^3} =\sqrt[3]{((3)/(5))^3}](https://img.qammunity.org/2021/formulas/mathematics/high-school/3mdlubj10594ppeei7v43v6ejujlw138z8.png)
Using property
![\sqrt[n]{a^n} =a](https://img.qammunity.org/2021/formulas/mathematics/high-school/47uuwhgsz6wrd2a89g3j3kn7rf82wvksre.png) , we will get:
, we will get:
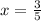
Therefore, the original voltage in the circuit is
 of a volt.
of a volt.