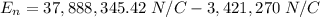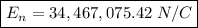Answer:
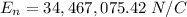
Explanation:
Electric Field
The electric field produced by a point charge Q at a distance d is given by
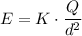
Where
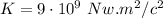
The net electric field is the vector addition of the individual electric fields produced by each charge. The direction is given by the rule: If the charge is positive, the electric field points outward, if negative, it points inward.
Let's calculate the electric fields of each charge at the given point. The first charge
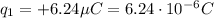 is at the origin. We'll calculate its electric field at the point x=-3.85 cm. The distance between the charge and the point is d=3.85 cm = 0.0385 m, and the electric field points to the left:
is at the origin. We'll calculate its electric field at the point x=-3.85 cm. The distance between the charge and the point is d=3.85 cm = 0.0385 m, and the electric field points to the left:
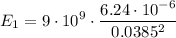
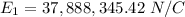
Similarly, for
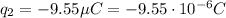 , the distance to the point is 12 cm + 3.85 cm = 15.85 cm = 0.1585 m. The electric field points to the right:
, the distance to the point is 12 cm + 3.85 cm = 15.85 cm = 0.1585 m. The electric field points to the right:
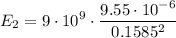
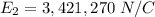
Since E1 and E2 are opposite, the net field is the subtraction of both