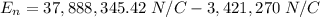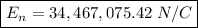Question

wo point charges lie on the $x$ axis. A charge of +6.24 $\mu C$ is at the origin, and a charge of -9.55 $\mu C$ is at $x$ = 12.0 cm. What is the net electric field at $x$ = -3.85 cm?

Answer 1

`E_n=34,467,075.42\ N/C`

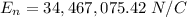
Explanation:

Electric Field

The electric field produced by a point charge Q at a distance d is given by

`\displaystyle E=K\cdot (Q)/(d^2)`

Where

`K = 9\cdot 10^9\ Nw.m^2/c^2`

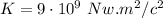
The net electric field is the vector addition of the individual electric fields produced by each charge. The direction is given by the rule: If the charge is positive, the electric field points outward, if negative, it points inward.

Let's calculate the electric fields of each charge at the given point. The first charge
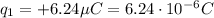`q_1=+6.24\mu C=6.24\cdot 10^(-6)C` is at the origin. We'll calculate its electric field at the point x=-3.85 cm. The distance between the charge and the point is d=3.85 cm = 0.0385 m, and the electric field points to the left:

`\displaystyle E_1=9\cdot 10^9\cdot (6.24\cdot 10^(-6))/(0.0385^2)`

`E_1=37,888,345.42\ N/C`

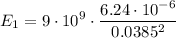
Similarly, for
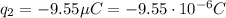`q_2=-9.55\mu C=-9.55\cdot 10^(-6)C`, the distance to the point is 12 cm + 3.85 cm = 15.85 cm = 0.1585 m. The electric field points to the right:

`\displaystyle E_2=9\cdot 10^9\cdot (9.55\cdot 10^(-6))/(0.1585^2)`

`E_2=3,421,270\ N/C`

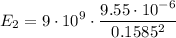
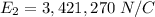
Since E1 and E2 are opposite, the net field is the subtraction of both

`E_n=37,888,345.42\ N/C-3,421,270\ N/C`

`\boxed{E_n=34,467,075.42\ N/C}`