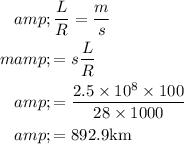Question

This elementary problem begins to explore propagation delayand transmission delay, two central concepts in data networking. Consider two hosts A andB, connected by a single link of rate R bps.suppose that the two hosts are separated by mmeters, and supose the propagation speed along the link is s meters/sec. Host A is to send a packet ofsize L bits to Host B.a. Express the propagation delay d(prop) interms of L and R.b. Determine the trnasmission time of the packet d(trans) in termsof L and R.c. Ignoring processing and queing delays obtain an expression forthe end to end delay.d. Supose Host A begins to transmit packet at time t=0 . At timet=d(trans) where is the last bit of the packet.e. Suppose d(prop)is greater than d(trans) . At time t= d(trans)where is the first bit of the packetf. Suppose d(prop)is less than d(trans) . At time t= d(trans) whereis the first bit of the packetg. Suppose s=2.5* 10power(8), L=100 bits and R=28 kbps. find thedistance m so tha d(prop) equals d(trans).

Answer 1

Step-by-step explanation:

(a)

Here, distance between hosts A and B is m meters and, propagation speed along the link is s meter/sec

Hence, propagation delay,
`d_(prop) = m/sec (s)`

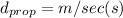
(b)

Here, size of the packet is L bits

And the transmission rate of the link is R bps

Hence, the transmission time of the packet,
`d_(trans) = L/R`

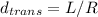
(c)

As we know, end-to-end delay or total no delay,

`\mathrm{d}_{\text {nodal }}=\mathrm{d}_{\text {proc }}+\mathrm{d}_{\text {quar }}+d_(\max )+d_{\text {prop }}`

`Here, $\mathrm{d}_{\text {rroc }}$ and $\mathrm{d}_{\text {quat }}$ \\Hence, $\mathrm{d}_{\text {rodal }}=\mathrm{d}_{\text {trass }}+\mathrm{d}_{\text {prop }}$ \\We know, $\mathrm{d}_{\text {trax }}=\mathrm{L} / \mathrm{R}$ sec and $\mathrm{d}_{\text {vapp }}=\mathrm{m} / \mathrm{s}$ sec`
`\text { Hence, } {d_{\text {nodal }}}=\mathrm{L} / \mathrm{R}+\mathrm{m} / \mathrm{s} \text { seconds }`

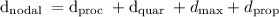
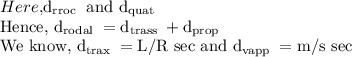
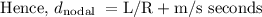
(d)

The expression, time
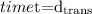`time $t=d_{\text {trans }}$` means the\at time since transmission started is equal to transmission delay.

As we know, transmission delay is the time taken by host to push out the packet.

Hence, at
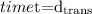`time $t=d_{\text {trans }}$` the last bit of the packet has been pushed out or transmitted.

(e)

If
`\ d_(prop) >d_(trans)`

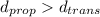
Then, at
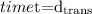`time $t=d_{\text {trans }}$` the bit has been transmitted from host A, but to condition (1), the first bit has not reached B.

(f)

If
`\ d_(prop) <d_(trans)`

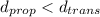
Then, at
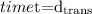`time $t=d_{\text {trans }}$`, the first bit has reached destination on B

Here,
`s=2.5 * 10^(8) \mathrm{sec}`

`\begin{aligned}&\mathrm{L}=100 \mathrm{Bits} \text { and }\\&\mathrm{R}=28 \mathrm{kbps} \text { or } 28 * 1000 \mathrm{bps}\end{aligned}`

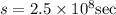
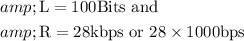
It's given that
`\ d_(prop) =d_(trans)`

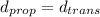
Hence,

`\begin{aligned}\ & (L)/(R)=(m)/(s) \\m &=s (L)/(R) \\&=(2.5 * 10^(8) * 100)/(28 * 1000) \\&=892.9 \mathrm{km}\end{aligned}`