Question

The​ half-life of polonium is 139​ days, but your sample will not be useful to you after 89​% of the radioactive nuclei present on the day the sample arrives has disintegrated. For about how many days after the sample arrives will you be able to use the​ polonium?

Answer 1

You will be able to use the sample for about 441 days.

Explanation:

The equation for the amount of polonium after t days is given by:

`P(t) = P(0)e^(-rt)`

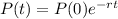
In which P(0) is the initial amount and r is the rate of decrease.

The​ half-life of polonium is 139​ days

This means that
`P(139) = 0.5P(0)`.

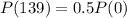We apply this to the equation, and find r.

`P(t) = P(0)e^(-rt)`

`0.5P(0) = P(0)e^(-139r)`

`e^(-139r) = 0.5`

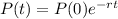
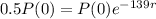
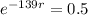
Applying ln to both sides of the equality:

`\ln{e^(-139r)} = ln(0.5)`

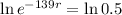
So

`-139r = ln(0.5)`

`139r = -ln(0.5)`

`r = -(ln(0.5))/(139)`

`r = 0.005`

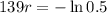
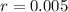
So

`P(t) = P(0)e^(-0.005t)`

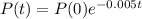
Your sample will not be useful to you after 89​% of the radioactive nuclei present on the day the sample arrives has disintegrated. For about how many days after the sample arrives will you be able to use the​ polonium?

It will be useful until t in which
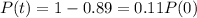`P(t) = 1-0.89 = 0.11P(0)`. So

`P(t) = P(0)e^(-0.005t)`

`0.11P(0) = P(0)e^(-0.005t)`

`e^(-0.005t) = 0.11`

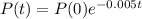
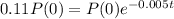
Applying ln to both sides

`\ln{e^(-0.005t)} = ln(0.11)`

`-0.005t = ln(0.11)`

`0.005t = -ln(0.11)`

`t = -(ln(0.11))/(0.005)`

`t = 441`

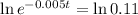
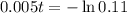
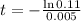
You will be able to use the sample for about 441 days.