Question

Find the length of BC.



Explain how you got it, please!
Thanks!

Answer 1

BC = 30.7 units (nearest tenth)

Explanation:

As ∠AQR = ∠CQR then ∠AQB = ∠CQD

This means that ΔABQ ~ ΔCDQ

Therefore, the side lengths of two similar triangles are proportional.

`\begin{aligned} \sf (AB)/(CD) & =\sf (BQ)/(QD)\\\sf \implies (32)/(19.2) & =\sf (15.0)/(QD)\\\sf \implies QD & = \sf 9 \end{aligned}`

Pythagoras' Theorem:
`\sf a^2+b^2=c^2`

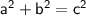
(where a and b are the legs, and c is the hypotenuse, of a right triangle)

Given:

• a = BD = BQ + QD = 15 + 9 = 24
• b = CD = 19.2
• c = BC

Substituting values into the formula:

`\begin{aligned}\sf 24^2+19.2^2 & = \sf BC^2\\\sf BC^2 & = \sf 944.64\\\sf BC & = \sf \pm√(944.64)\\\sf BC & = \sf 30.7 \ (nearest \ tenth)\end{aligned}`

(since distance is positive only)

Answer 2

BC = 30.73

Here,

`\sf (AB)/(BQ) = (CD)/(DQ)`

so first solve for QD

`\sf \hookrightarrow (32)/(15) = (19.2)/(DQ)`

`\sf \hookrightarrow 32(DQ)} =19.2(15)`

`\sf \hookrightarrow 32(DQ)} =288`

`\sf \hookrightarrow DQ =9`

• Hence, QD = 9

Now! using Pythagoras theorem,

• CD² + BD² = BC²

• 19.2² + (9+15)² = BC²

• BC = √368.64+576

• BC = 30.73499634

• BC = 30.73 ( rounded to nearest hundredth )