Answer:
Exact value of Cos(45° - 60°) is 0.96 using difference of two angles.
Explanation:
Given:
Cos(45° - 60°)
We have to apply the formula of cosine for difference of the two angles.
Formula:

Plugging the values.
⇒
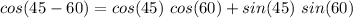
We know that the values :
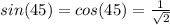
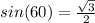 and
and
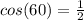
So,
⇒

⇒
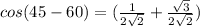
⇒
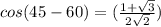
⇒
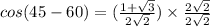 ...rationalizing
...rationalizing
⇒
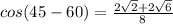
⇒
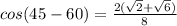 ...taking 2 as a common factor
...taking 2 as a common factor
⇒

To find the exact values we have to put the values of sq-rt .
As,
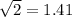 and
and
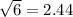
Then
⇒
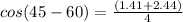
⇒
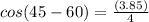
⇒
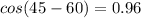
So the exact value of Cos(45° - 60°) is 0.96 using difference of two angles.