Question

In a class of 30 students, there are 17 girls and 13 boys. Five are A students, and three of these students are girls. If a student is chosen at random, what is the probability of choosing a girl or an A student?

Answer 1

0.634 is the required probability.

Explanation:

We are given the following in the question:

Total number of students = 30

Number of girls = 17

`n(G) =17`

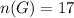
Number of boys = 13

`n(B) = 13`

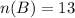
Number of A students = 5

`n(A) = 5`

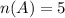
Number of A students that are girl = 3

`n(A\cap G) = 3`

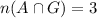
We have to find the probability choosing a girl or an A student.

We evaluate:

`n(A\cup G) = n(A) + n(G) - n(A\cap G) = 5 + 17-3 = 19`

`\text{Probability} = \displaystyle\frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}`

`P(A\cup G) = (n(A\cup G) )/(30) = (19)/(30) = 0.634`

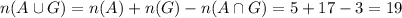
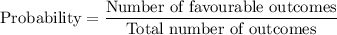
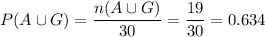
0.634 is the probability of choosing a girl or an A student.