Question

Please help solve this

Answer 1

(i) The value of
`_9C_9` is 1

(ii) The value of
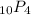`_(10)P_4` is 5040

Step-by-step explanation:

(i)Given that the combination is
`_9C_9`

We need to evaluate the combination
`_9C_9`

The formula to find the combination is given by

`_nC_r=(n!)/((n-r)!r!)`

Let us use this formula to evaluate
`_9C_9`

Thus, we have,

`_9C_9=(9!)/((9-9)!9!)`

Simplifying, we have,

`_9C_9=(9!)/((0)!9!)`

Cancelling the terms, we get,

`_9C_9=1`

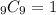
Thus, the value of
`_9C_9` is 1

(ii) Also, given that the permutation
`_(10)P_4`

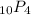
We need to evaluate the permutation
`_(10)P_4`

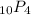
The formula to find the permutation is given by

`_nP_r=(n!)/((n-r)!)`

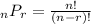
Let us use this formula to evaluate
`_(10)P_4`

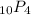
Thus, we have,

`_(10)P_4=(10!)/((10-4)!)`

Simplifying, we get,

`_(10)P_4=(10!)/(6!)`

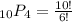
Expanding, we get,

`_(10)P_4=(10*9*8*7*6!)/(6!)`

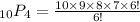
Cancelling the common terms, we get,

`_(10)P_4=10*9*8*7`

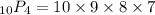
simplifying, we get,

`_(10)P_4=5040`

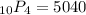
Thus, the value of
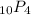`_(10)P_4` is 5040