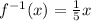Question

If f(x) = 5x, what is f^-1 (x)

Answer 1

The inverse of the function is
`f^(-1)(x)=(1)/(5)x`

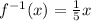
Explanation:

The given function is
`f(x)=5x`

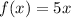
We need to determine the inverse of the function
`f^(-1)(x)`

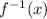
The inverse of the function can be determined by interchanging the variables x and y.

Let us interchange the variables x and y in the function
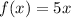`f(x)=5x`, we have,

`x=5y`

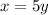
To find the inverse of the function, let us solve for y.

Hence, dividing both sides of the equation by 5, we get,

`(1)/(5)x=y`

This is the inverse of the function
`f(x)=5x`

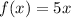
Therefore, the inverse of the function is
`f^(-1)(x)=(1)/(5)x`