Question

A fence is guarding off a vegetable garden in the form of a rectangle. It has one side that is 10m greater than the other side. Find the length of the fence needed to surround this garden if the area of the vegetable garden is 2184m2.

Answer 1

188

Explanation:

Sorry, I’m bad at explaining

Answer 2

The length of the fence needed to surround this garden is 188 meters.

Explanation:

Given : A fence is guarding off a vegetable garden in the form of a rectangle. It has one side that is 10 m greater than the other side.

To find : The length of the fence needed to surround this garden if the area of the vegetable garden is 2184 m² ?

Solution :

Let the one side of rectangle be 'x'.

Then the other side is 'x+10'.

The area of the rectangle is 2184 m²,

i.e.
`x(x+10)=2184`

`x^2+10x-2184=0`

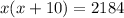
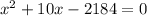
Solve by middle term split,

`x^2+52x-42x-2184=0`

`x(x+52)-42(x+52)=0`

`(x+52)(x-42)=0`

`x=-52,42`

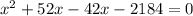
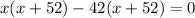
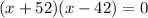
Reject negative value,

The side of the rectangle is 42 m.

The other side is 42+10=52 m

The perimeter of the rectangle is
`P=2(l+b)`

`P=2(42+52)`

`P=2(94)`

`P=188`

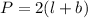
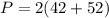
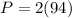
Therefore, the length of the fence needed to surround this garden is 188 meter.