Answer:
a. This option is correct
b. This will be true only if we take the mode as the best representative value
c. This is a not correct choice
d. This option is correct
Explanation:
Statistics
We are given a dot plot representing 30 random sample proportions of high school students about their sports activities. Based on the data extracted from the plot, we can make some basic conclusions and, less accurately, some predictions.
From the data plot we can see that the following proportions were obtained, along with their absolute frequencies:
0.05 -> 3
0.10 -> 8
0.15 -> 7
0.20 -> 5
0.25 -> 4
0.30 -> 2
Let's select which of the following options are correct
a. A sample proportion of 0.20 means that 4 of 20 high school students responded that they play a sport.
The ratio between the sport playing students to the total of high school students is
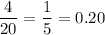
Thus, this statement is correct.
b. The best prediction for the proportion of all high school students that play a sport is 0.10.
This will be true only if we take the mode as the best representative value for the whole dataset. Personally, I don't like to trust the mode as a good central tendency result, I'd prefer the mean instead.
c. The mean of the 30 sample proportions calculated to the nearest hundredth is 0.16
Computing the mean of the sample proportions
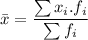
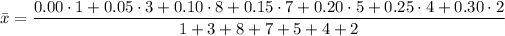
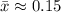
This choice is not correct.
d. The shape of the sample distribution is fairly symmetrical
We can see the distribution if a little left-skewed but it can be assumed as fairly symmetrical.
This choice is correct