Question

An elevator and its load have a combined mass of 1650 kg. Find the tension in the supporting cable when the elevator, originally moving downward at 11 m/s, is brought to rest with constant acceleration in a distance of 41 m.

Answer 1

Tension in the supporting cable is = 4,866 N ≅4.9 KN

Step-by-step explanation:

First of all, we need to understand that tension is a force, so the motion law

F = Ma applies perfectly.

From Newtons third law of motion, action and reaction are equal and opposite. This means that the force experienced by the elevator, is equal to the tension experienced by the spring.

Parameters given:

Mass of load = 1650 kg

Acceleration of load = ?

The acceleration of the load can be obtained by diving the change in velocity by the time taken. But we need to know the time taken for the motion to 41 m.

Time taken = distance covered / velocity

=
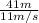`(41m)/(11m/s)` = 3.73 seconds

∴Acceleration = ( initial velocity - final velocity )/ time taken

Note: Final velocity is = 0 since the body came to a rest.

Acceleration =
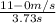`(11 - 0 m/s)/(3.73s)` = 2.95m/
`s^(2)`

Force acting on the cable = mass of elevator × acceleration of elevator

= 1650 × 2.95 = 4869.5 kg ≅ 4.9 KN