Question

The number of failures of a testing instrument from contamination particles on the product is a Poisson random variable with a mean of 0.012 failures per hour. (a) What is the probability that the instrument does not fail in an 8-hour shift? (b) What is the probability of at least 1 failure in a 24-hour day?

Answer 1

a) 0.9084

b) 0.2502

Explanation:

We are given the following in the question:

The number of failures follows a Poisson distribution with mean

`\mu = 0.012`

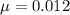
Formula:

`P(X =k) = \displaystyle(\lambda^k e^(-\lambda))/(k!)\\\\ \lambda \text{ is the mean of the distribution}`

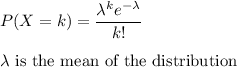
a) probability that the instrument does not fail in an 8-hour shift

`\lambda = 0.012* 8 = 0.096`

We have to evaluate:

`P(x = 0) = \displaystyle((0.096)^0 e^(-0.096))/(0!) = 0.9084`

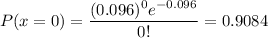
0.9084 is the probability that the instrument does not fail in an 8-hour shift

b) probability of at least 1 failure in a 24-hour day

`\lambda = 0.012* 24 = 0.288`

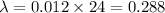
We have to evaluate:

`P(x \geq 1) =1-P(x=0) =1-\displaystyle((0.288)^0 e^(-0.288))/(0!) = 0.2502`

0.2502 is the probability of at least 1 failure in a 24-hour day.