Final answer:
The rate of change of the height of the water in the pool is approximately 0.2124 feet per minute.
Step-by-step explanation:
To find the rate of change of the height of the water in the pool, we can use the formula for the volume of a cylinder:
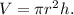
The rate of change of the height, dh/dt, can be found by differentiating both sides of this equation with respect to time. Since the rate of change of the volume, dV/dt, is given to be 6 cubic feet per minute, we can substitute the values of r, h, and dV/dt into the equation and solve for dh/dt.
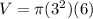
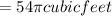
dV/dt = 6 cubic feet per minute
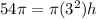
h = 6 feet
Now, we can use the equation: dV/dt = π(r^2)(dh/dt) and solve for dh/dt.


= 0.2124 feet per minute