Answer:
Therefore,
The greatest number of paper cups that can be completely filled from the water cooler is 446 cups.
Explanation:
For Cylinder Cooler
Radius = r₁ = 9 in
Height = h₁ = 22 in
For Cone Cups,
Radius = r₂ = 2 in
Height = h₂ = 3 in
To Find:
Number of Paper Cups = ?
Solution:
For a Cylinder we know that
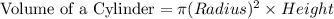
And For a Cone,
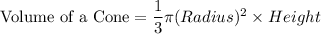
Now number of paper cups that can be completely filled from the water cooler will be given as
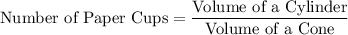
Substituting the values we get

Substituting the values we get
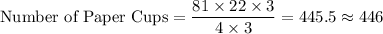
Therefore,
The greatest number of paper cups that can be completely filled from the water cooler is 446 cups.