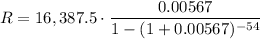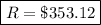Question

You are interested in purchasing a used car for $17,250. The dealer offers financing at a rate of 6.8% APR when the purchase is financed for 54 months. If you make a 5% down payment, what would the monthly payment be for this purchase?

Answer 1

The monthly payments will be $353.12

Step-by-step explanation:

Financing

When a purchase is made at present value and the payment will be financed at a rate of interest i for n periods, the present value PV is

`\displaystyle PV=R\cdot (1-(1+i)^(-n))/(i)`

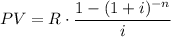
where R is the regular payment (usually monthly).

Solving for R

`\displaystyle R=PV\cdot (i)/(1-(1+i)^(-n))`

It's important to recall than only the unpaid amount goes financing, if some down-payment is made, it must be subtracted from the PV to be financed.

The present value of the car is 17,250 from which the buyer will make a 5% down-payment. It means that the real financing amount is

`PV=17,250\cdot 95\%=16,387.5`

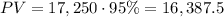
The rate of interest is

`i=6.8\%=6.8/(12\cdot 100)=0.00567`

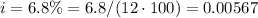
It also follows that n=54.

Computing R

`\displaystyle R=16,387.5\cdot (0.00567)/(1-(1+0.00567)^(-54))`

`\boxed{R=\$353.12}`