Question

A circle has the equation 2x2+12x+2y2−16y−150=0. Jerene must convert the equation to standard form. She writes a description of the steps she can take to convert the equation, but she is missing some information. Step 1: Divide each term by 2 so that the coefficient of x2 and y2 will be 1. Step 2: Add _[blank 1]_ to both sides. Step 3: Add _[blank 2]_ to both sides to complete the square for the x's. Step 4: Add _[blank 3]_ to both sides to complete the square for the y's. Step 5: Factor the trinomial of the x's and rewrite as a perfect square, _[blank 4]_. Step 6: Factor the trinomial of the y's and rewrite as a perfect square, _[blank 5]_. Step 7: The standard form of the equation is _[blank 6]_.

Answer 1

Step 1: Divide each term by 2

x2+6x+y2−8y−75=0

BLANK 1: add 75 to both sides

x2+6x+y2−8y−75+75=+75

x2+6x+y2−8y=75

BLANK 2: add 9 to both sides to complete the squares for the x's

x2+6x+9+y2−8y=84

BLANK 3: add 16 to both sides to complete the squares for the y's

x2+6x+9+y2−8y+16=100

Step 5: Rewrite x's as a perfect square

`x^(2)+6x+9= (x+3)^(2)`

Step 6: Rewrite y's as a perfect square

`y^(2)-8y-16=(y-4)^(2)`

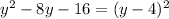
Step 7:

Standard form of the equation:
`(x+3)^(2)+(y-4)^(2)=100`