Answer:
7500 revolutions
Step-by-step explanation:
Given:
Time taken for the centrifuge (t) = 3 min
Initial angular speed of the centrifuge (ω₁) = 0 rad/min (Initially at rest)
Final rotational speed (N₂) = 5000 rpm
So, final angular speed of the centrifuge is given as:
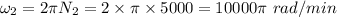
Now, using the concept of angular motion, the angular acceleration is given as:
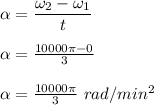
Now, angular displacement of the centrifuge is determined using the angular equation of motion which is given as:
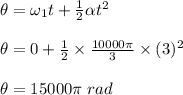
Now, we know that, 1 revolution corresponds to a angular displacement of 2π radians.
So, 2π rad = 1 revolution
∴ 15000π rad =
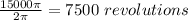
Therefore, the centrifuge makes 7500 revolutions.