Question

A boat takes 5 hours to go upstream. It can go 50 miles downstream in the same time. Find the rate of the current in the rate of the boat in Still water.

Answer 1

Rate of current is 3 miles per hour and speed of the boat in still water is 7 miles per hour.

Explanation:

This question is incomplete; find the complete question here.

A boat travels 20 miles upstream in 5 hours. Going downstream, it can travel 50 miles in the same amount of time. Find the speed of the current and the speed of the boat in still water.

Let the speed boat in the still water = x miles per hour

and the speed (rate) of the current = y miles per hour

Speed of the boat to go upstream (against the current) will be = (x - y)miles per hour

Since boat takes 5 hours downstream to travel 50 miles then from the formula,

`\text{Time}=\frac{\text{Distance}}{\text{Speed}}`

`5=(50)/((x+y))`

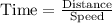
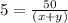
(x + y) = 10 -------(1)

Boat takes 5 hours to travel 50 miles upstream then,

`\text{Time}=\frac{\text{Distance}}{\text{Speed}}`

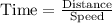
5 =
`(20)/((x-y))`

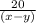
x - y = 4 -----(2)

By adding equation (1) and question (2)

(x + y) + (x - y) = 14

2x = 14

x = 7 miles per hour

From equation (1),

7 + y = 10

y = 3 miles per hour

Therefore, Rate of current is 3 miles per hour and speed of the boat in still water is 7 miles per hour.