Question

A triangle has three sides 35cm 54 cm and 61 cm find its area Also find the smallest of its altitude ​

Answer 1

Area of given triangle is 939.15cm² and smallest altitude is 30.8cm

Solution:

We are given three sides of a triangle, Let the sides be :

• ( a ) = 35 cm

• ( b ) = 54 cm

• ( c ) = 61 cm

We can find the area of the triangle with its three sides using Heron's Formula

• Heron's Formula

Heron's formula was founded by hero of Alexandria, for finding the area of triangle in terms of the length of its sides. Heron's formula can be written as:

`\sf{ \pmb { \longrightarrow \: √(s(s - a)(s - b)(s - c)) }}`

where ( s ) :

`\sf \longrightarrow s = (a + b + c)/(2)`

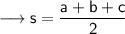
Therefore, for the given triangle first we will calculate ( s )

`\begin {aligned}\quad & \quad \longmapsto \sf s = (a + b + c)/(2) \\ & \quad \longmapsto \sf s = (35 + 54 + 61)/(2) \\ & \quad \longmapsto \sf s = (150)/(2) \\ & \quad \longmapsto \sf s = 75cm \end{aligned}`

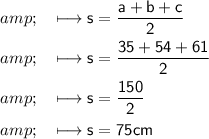
Now, Area of triangle will be:

`\begin{aligned}&:\implies \sf\quad \sf \: A = √(s(s - a)(s - b)(s - c)) \\ &:\implies \sf\quad \sf \: A = √(75(75 - 35)(75 - 54)(75 - 61)) \\&:\implies \sf\quad \sf \: A = √(75 * 40 * 21 * 14) \\ &:\implies \sf\quad \sf \: A = √(5 * 5 * 3 * 3 * 2 * 2 * 7 * 7 * 2 * 2 * 5) \\ &:\implies \sf\quad \sf \: A =5 * 3 * 2 * 7 * 2 √(5) \\ &:\implies \sf\quad \sf \: A =420 * 2.23 \\ &:\implies \sf\quad \sf \boxed{ \pmb{ \sf A =939.15 {cm}^(2) }} \end{aligned}`

Also, we have to find the smallest altitude, and the smallest altitude will be on the longest side. So,

`\begin{aligned}&:\implies \sf\quad \sf \: Area =939.15 \\ &:\implies \sf\quad \sf \: (1)/(2) * b * h =939.15 \\ &:\implies \sf\quad \sf \: (1)/(2) * 61 * h = 939.15 \\&:\implies \sf\quad \sf \: h =939.15 * (2)/(61) \\&:\implies \sf\quad \sf \: h = (1818.3)/(61) \\ &:\implies \sf\quad \boxed{ \pmb{\sf \: h =30.79 \: (approx)}} \end{aligned}`

Answer 2

Area = 939.15 cm² (2 d.p.)

Shortest Altitude = 30.79 cm (2 d.p.)

Explanation:

Heron's Formula allows us to find the area of a triangle in terms its side lengths.

Heron's Formula

`\sf Area = √(s(s-a)(s-b)(s-c))`

where:

• a, b and c are the side lengths of the triangle
• s is half the perimeter

Given values:

• a = 35 cm
• b = 54 cm
• c = 61 cm

Find the value of s:

`\sf \implies s=(a+b+c)/(2)=(35+54+61)/(2)=75\:cm`

Substitute the values into the formula and solve for area:

`\begin{aligned}\implies \sf Area & =\sf √(75(75-35)(75-54)(75-61))\\& = \sf √(75(40)(21)(14))\\& = \sf √(882000)\\& = \sf √(176400 \cdot 5)\\& = \sf √(176400)√(5)\\& = \sf 420√(5)\\& = \sf 939.15\:\:cm^2\:\:(2\:d.p.)\end{aligned}`

The altitude of a triangle is a perpendicular line segment drawn from a vertex of the triangle to the side opposite to it.

The shortest altitude of a triangle is drawn to the longest side.

Therefore, the shortest altitude will be the height of the triangle when the longest side is the base:

`\begin{aligned}\textsf{Area of a Triangle} & = \sf (1)/(2) * base * height\\\implies \sf 420√(5) & = \sf (1)/(2) * 61 * altitude \\\implies \sf Altitude & = \sf (2 \cdot 420√(5))/(61)\\& = \sf (840√(5))/(61)\\ & = \sf 30.79\:\:cm\:\:(2\:d.p.)\end{aligned}`