Question

Consider the following hypotheses:

H0: ? ? 12.6

HA: ? > 12.6
A sample of 25 observations yields a sample mean of 13.4. Assume that the sample is drawn from a normal population with a known population standard deviation of 3.2.

a. Calculate the p-value. (Round "z" value to 2 decimal places and final answer to 4 decimal places.

p-value =
b. What is the conclusion if ? = 0.10

A. Reject H0 since the p-value is greater than ?.
B. Reject H0 since the p-value is smaller than ?.
C. Do not reject H0 since the p-value is greater than ?.
D. Do not reject H0 since the p-value is smaller than ?.

c.Calculate the p-value if the above sample mean was based on a sample of 100 observations. (Round "z" value to 2 decimal places and final answer to 4 decimal places.)

p-value =

d. What is the conclusion if ? = 0.10?

A. Reject H0 since the p-value is greater than ?.
B. Reject H0 since the p-value is smaller than ?.
C. Do not reject H0 since the p-value is greater than ?.
D. Do not reject H0 since the p-value is smaller than ?.

Answer 1

Explanation:

Given that a hypothesis test (right tailed) was conducted for comparing sample mean with population mean.

`H0: \bar x = 12.6\\HA: \bar x > 12.6`

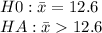
Sample size n = 25

Population std dev =
`\sigma = 3.2`

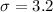
Std error of sample mean = sigma/sqrt n = 3.2/5 = 0.64

Sample mean = 13.4

Mean difference = 13.4-12.6 = 0.80

since population std deviation is known we can use Z test

Z= mean diff/std error = 1.25

a) p valu e= 0.10565

= 0.1057

b) Since p value is >0.10 accept H0.

C. Do not reject H0 since the p-value is greater than 0.10

c) If n =100, then we have std error of mean = 1/2 original = 0.32

Test statistic = 0.8/0.32 = 2.5

p value = 0.00621

d) Here since p <0.10, we reject null hypotehsis

B. Reject H0 since the p-value is smaller than 0.10