Question

Lots of 40 components each are deemed unacceptable if they contain 3 or more defectives. The procedure for sampling a lot is to select 5 components at random and to reject the lot if a defective is found. a) What is the probability that exactly 1 defective is found in the sample if there are 3 defectives in the entire lot? Find the mean and variance of the number of defective components in the selected 5 and then use Chebyshev's theorem to interpret the interval b) t 2

Answer 1

The probability of founding exactly one defective item in the sample is P=0.275.

The mean and variance of defective components in the sample are:

`\mu=0.375\\\\\sigma^2=0.347`

Explanation:

In the case we have a lot with 3 defectives components, the proportion of defectives is:

`p=3/40=0.075`

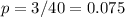
a) The number of defectives components in the 5-components sample will follow a binomial distribution B(5,0.075).

The probability of having one defective in the sample is:

`P(k=5)=\binom{5}{1}p^1(1-p)^4=5*0.075*0.925^4=0.275`

b) The mean and variance of defective components in the sample is:

`\mu=np=5*0.075=0.375\\\\\sigma^2=npq=5*0.075*0.925=0.347`

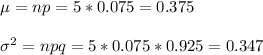
The Chebyschev's inequality established:

`P(|X-\mu|\geq k\sigma)\leq (1)/(k^2)`