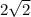Question

or the function f(x)=x− 5 x , find all values of c in the interval [2,4] that satisfy the conclusion of the Mean-Value Theorem. If appropriate, leave your answer in radical form. Enter all fractions in lowest terms

Answer 1

Therefore the value of c is
`2\sqrt {2}`

Explanation:

Mean Value Theorem:

It state that if f(x) is defined

(i) f(x) continuous on the interval [a,b]

(ii) f(x) differentiable on (a,b).

then there exist a one number c∈ (a,b) such that

`f'(c)=(f(b)-f(a))/(b-a)`

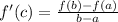
Here
`f(x)= x-\frac {5}{x}`

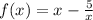
(i) f(x) is continuous on [2,4]

Since it is discontinuous at 0 and 0∉[2,4].

(ii)
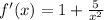`f'(x) = 1+(5)/(x^2)` which is exist x≠0 and 0∉(2,4).

Therefore f(x) is differentiable on (2,4)

f(x) satisfies the Mean Value Theorem,

Then there exist a number c∈(2,4) such that

`f'(c)=(f(4)-f(2))/(4-2)`

`\Rightarrow 1+(5)/(c^2)=(4-(5)/(4)-(2-(5)/(2)))/(4-2)`

`\Rightarrow 1+(5)/(c^2) = (2+(5)/(4))/(2)`

`\Rightarrow 1+(5)/(c^2)=1+(5)/(8)`

`\Rightarrow c^2 = 8`

`\Rightarrow c= 2\sqrt {2}`

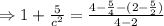
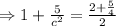
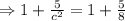
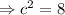
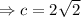
Therefore the value of c is
`2\sqrt {2}`