Question

A fair pair of dice is rolled and the sum of the points is noted. What is the probability that one of the dice results in a point of 4​, given that the sum of the points is 6​?

Answer 1

The needed probability is 0.4.

Explanation:

Here, given that two fair dices are rolled.

The sum of both the numbers on the dice = 6

Also, number on one of the dice = 4

Let us write the given possibilities.

The outcomes when ("one of the dice shows 4") are: (2, 4) and (4, 2)

The outcomes when ("given that the sum of the dice is 6") are:

(1, 5) , (2, 4) , (3, 3), (4, 2) and (5, 1)

As we can see from the above information, that the total outcomes when the sum of digits is 6 is 5.

Also, the favorable outcomes = 2

So, there are total 2 out of 5 events which are desirable to given condition.

So, the required probability =
`\frac{\textrm{The number of desirable events}}{\textrm{Total number of events}} = (2)/(5) = 0.4`

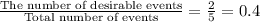
Hence, the needed probability is 0.4.