Answer:
In total,
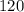 permutations of three items can be selected from a group of six distinct elements.
permutations of three items can be selected from a group of six distinct elements.
In particular, there are
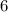 ways to order three distinct items.
ways to order three distinct items.
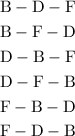 .
.
Explanation:
The formula
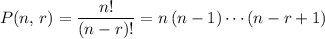 gives the number of ways to select and order
gives the number of ways to select and order
 items from a group of
items from a group of
 distinct elements.
distinct elements.
To select and order three items from a group six distinct elements, let
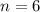 and
and
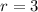 . Apply the formula:
. Apply the formula:
 .
.
In other words, there are
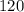 unique ways to select and order three items (select a permutation of three items) from a group of six distinct elements.
unique ways to select and order three items (select a permutation of three items) from a group of six distinct elements.
Consider: what's the number of ways to order three distinct items? That's the same as asking: how many ways are there to select and order three items from a group of three distinct elements? Let
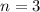 and
and
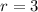 . Apply the formula for permutation:
. Apply the formula for permutation:
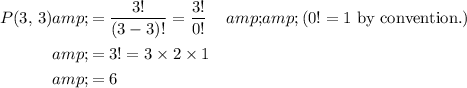 .
.
To find the permutations, start by selecting one element as the first of the list. A tree diagram might be helpful. Refer to the attachment for an example.