Answer:
Correct option: B
Explanation:
The professor can perform a One-mean t-test to determine whether the average score of the students in his class is more than the average score of all the students attending university.
A t-test will be used instead of the z-test because the population standard deviation is not provided instead it is estimated by the sample standard deviation.
The hypothesis for this test can be defined as follows:
H₀: The average score of the students in his class is not more then the entire university, i.e. μ ≤ 35.
Hₐ: The average score of the students in his class is more then the entire university, i.e. μ > 35.
Given:
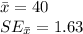
The test statistic is:
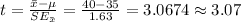
Thus, the correct option is (B).