Final answer:
The acceleration of the car when its velocity is 12.0m/s is 6.226m/s^2.
Step-by-step explanation:
The acceleration of the car can be found by taking the derivative of the velocity function. Since the velocity function is given by
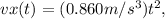
with respect to time to get the acceleration function
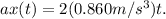
when vx = 12.0m/s, we substitute vx = 12.0m/s into the velocity function and solve for t:
12.0m/s = (0.860m/s^3)t^2.
Dividing both sides by 0.860m/s^3 gives us t^2 = 13.95, and taking the square root of both sides gives us t = ±3.73s.
Since time cannot be negative, we discard the negative value and conclude that the car takes approximately 3.73 seconds to reach a velocity of 12.0m/s. Now we can substitute this value of t into the acceleration function to find the acceleration at this time: ax(3.73s) = 2(0.860m/s^3)(3.73s) = 6.226m/s^2.