Answer:
So, the sample standard deviation is 7.1.
Explanation:
From Exercise we have the next numbers: 2, 6, 15, 9, 11, 22, 1, 4, 8,19.
So, N=10, because we have 10 numbers.
We use the formula for standard deviation:
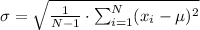
So, μ is the mean of all our values.
We get:

Now, we calculate the sum
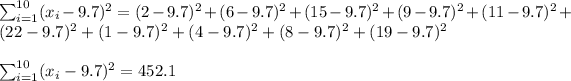
Therefore, we get
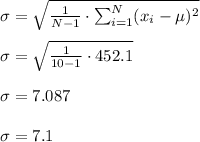
So, the sample standard deviation is 7.1.