Question

According to a Pew Research survey, about 27% of American adults are pessimistic about the future of marriage and the family. This is based on a sample, but assume that this percentage is correct for all American adults. Using a binomial model, what is the probability that, in a sample of 20 American adults, 25% or fewer of the people in the sample are pessimistic about the future of marriage and family?

Answer 1

P(X≤5)=0.5357

Explanation:

Using the binomial model, the probability that x adults from the sample, are pessimistic about the future is calculated as:

`P(x)=(n!)/(x!(n-x)!) *p^(x)*(1-p)^(n-x)`

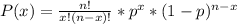
Where n is the size of the sample and p is the probability that an adult is pessimistic about the future of marriage and family. So, replacing n by 20 and p by 0.27, we get:

`P(x)=(20!)/(x!(20-x)!)*0.27^(x)*(1-0.27)^(20-x)`

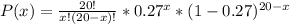
Now, 25% of 20 people is equal to 5 people, so the probability that, in a sample of 20 American adults, 25% or fewer of the people are pessimistic about the future of marriage and family is equal to calculated the probability that in the sample of 20 adults, 5 people of fewer are pessimistic about the future of marriage and family.

Then, that probability is calculated as:

P(X≤5)= P(1) + P(2) + P(3) + P(4) + P(5)

Where:

`P(0)=(20!)/(0!(20-0)!)*0.27^(0)*(1-0.27)^(20-0)=0.0018`

`P(1)=(20!)/(1!(20-1)!)*0.27^(1)*(1-0.27)^(20-1)=0.0137`

`P(2)=(20!)/(2!(20-2)!)*0.27^(2)*(1-0.27)^(20-2)=0.0480\\P(3)=(20!)/(3!(20-3)!)*0.27^(3)*(1-0.27)^(20-3)=0.1065\\P(4)=(20!)/(4!(20-4)!)*0.27^(4)*(1-0.27)^(20-4)=0.1675\\P(5)=(20!)/(5!(20-5)!)*0.27^(5)*(1-0.27)^(20-5)=0.1982`

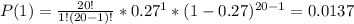
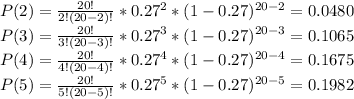
Finally, P(X≤5) is equal to:

P(X≤5) = 0.0018+0.0137 + 0.0480 + 0.1065 + 0.1675 + 0.1982

P(X≤5) = 0.5357