Answer:
(a) Given that a chip passes the test, what is the probability that it is a good chip?
LetB = {the chip is good}
A={the chip passes the cheap test}.
Bc={the chip is bad}
Ac={the chip fails the cheap test}
P(A | B) = 1
P(A | B c ) = 0.075
=
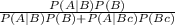 =
=
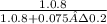 ≈ 0.9751
≈ 0.9751
(b) If the company sells all chips that pass the cheaper test, what percentage of sold chips will be bad?
P(B c |A) = 1 − P(B | A) = 1 - 0.9751 = 0.0249