Answer:
Area of given triangle is 939.15cm² and smallest altitude is 30.8cm
Solution:
We are given three sides of a triangle, Let the sides be :
We can find the area of the triangle with its three sides using Heron's Formula
Heron's formula was founded by hero of Alexandria, for finding the area of triangle in terms of the length of its sides. Heron's formula can be written as:
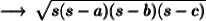
where ( s ) :
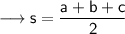
Therefore, for the given triangle first we will calculate ( s )
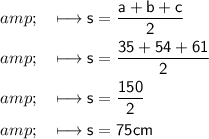
Now, Area of triangle will be:

Also, we have to find the smallest altitude, and the smallest altitude will be on the longest side. So,
